Étude des actions de groupe — Partie 1 : Rappels

Cet article fait partie d’une série sur les actions de groupe.

---

Je vais tâcher ici de vous expliquer en des termes simples les concepts dont il est question afin de vous en donner une idée, et vous orienter vers des ressources plus adaptées si vous avez envie d’en savoir plus.

Avertissement : mes explications ne sauraient remplacer un véritable cours de mathématiques. En particulier, elles contiennent des simplifications abusives de certaines définitions.

Structures algébriques

Comment expliquer les structures algébriques de manière basique ? Je vais reprendre l’introduction d’un de mes anciens professeurs de maths : prenez du popcorn, ça en vaut la peine.

Vision schématique

Le principe de base de l’algèbre est le suivant :

• Prenez un machin qui possède des règles internes.
• En considérant seulement une partie du machin qui respecte les mêmes règles, on obtient un sous-machin.
• Une application d’un machin dans un autre machin qui conserve leurs règles respectives est un morphisme de machins.
• La plus petite partie d’un machin qui contient un élément \( e \) est le sous-machin engendré par \( e \).

Félicitations, vous avez compris l’algèbre. Dans ses grandes lignes.

Quelques précisions

Soyons un peu plus précis maintenant : quels genres de machins les mathématiciens considèrent-ils ?

Globalement, il y a les groupes, les anneaux et les corps. Je vais détailler un peu les groupes puis je vais juste expliquer brièvement ce que sont les autres structures.

Pour rappel, le symbole \( \forall \) signifie “pour tout”, et le symbole \( \exists \) signifie “il existe”.

Loi interne

Définissons les opérations rigoureusement : on appelle loi interne sur un ensemble \( E \) une application de \( E \times E \) dans E.

Par exemple, l’addition dans l’ensemble des entiers naturels \( \mathbb{N} \) est une loi interne : elle prend deux entiers et en donne un autre. \( 2 + 3 = 5, \) facile non ?

Groupes

Un groupe est un ensemble \( G \) muni d’une loi interne \( * \) telle que :

1. \( * \) est associative :
   \[ \forall x,y,z \in G, (x * y) * z = x * (y * z) \]
2. \( (G, *) \) possède un élément neutre : il existe \( e \in G \) tel que \[ \forall x \in G, x * e = x = e * x \]
3. Tout élément de \( G \) est inversible pour \( * \) :
   \[ \forall x \in G, \exists h \in G: h * x = e = x * h\]

Par exemple, l’ensemble \( \mathbb{Z} \) des entiers relatifs muni de la loi \( + \) est un groupe.
En effet :

1. \( + \) est bien associative.
2. 0 est neutre pour \( + \).
3. Pour tout \( n \in \mathbb{Z}, -n \) est un inverse.

Anneaux

Pour faire simple, les anneaux sont des groupes avec une seconde loi interne compatible avec la première (distributive, précisément). Vous vous rappelez de la leçon de collège où on vous expliquait que la multiplication est distributive sur l’addition ? Mais si, c’est la règle qui permet ce genre de calcul : \[ x * (y + z) = x * y + x * z \] Eh bien c’est le même concept !
Justement, on appelle généralement la première loi interne addition et la seconde loi interne multiplication, et les éléments neutres pour addition et multiplication sont respectivement appelés \( 0 \) et \( 1 \).

Corps

Les corps sont des anneaux plus “gentils” que les autres : tout élément non nul est inversible pour les deux loi internes.

Les corps sont un peu les bons élèves des ensembles : ils font tout comme il faut, pas de surprise avec eux. Ça se comprend bien : plus on met de contraintes, moins il y a d’éléments perturbateurs. Si les groupes sont en T-shirt et les anneaux en chemise, les corps sont en smoking avec nœud papillon.

En anecdote, vous vous demandez sûrement dans quelles structures on retrouve la soustraction et la division. En fait, nul besoin de les définir : la soustraction de \( x \) est juste l’addition de son inverse pour l’addition, géneralement noté \( -x \), et la division par \( x \) est la multiplication par son inverse pour la multiplication, généralement noté \( x^{-1} \).

Retour sur les machins

Vous pouvez remplacer machin par n’importe lequel des trois noms ci-dessus ! Essayons avec groupe.

• Un sous-groupe \( H \) d’un groupe \( (G, *) \) est une partie de \( G \) qui conserve ses trois propriétés et est stable par la loi interne \( * \) et par passage à l’inverse. Pour faire simple, tout ce qui se passe dans \( H \) reste dans \( H, \) un peu comme dans le Fight Club.

• Un morphisme de groupe de \( (\mathbb{R}, +) \) dans \( (\mathbb{R}_+^*, \times) \) est l’exponentielle, car elle conserve leurs opérations. En effet, elle verifie la formule : \[ \exp(a+b) = \exp(a) \times \exp(b) \]

• En se plaçant dans \( (\mathbb{R}, +), \) le sous-groupe engendré par 1 est \( \mathbb{N} \). En effet, c’est le plus petit sous-groupe de \( \mathbb{R} \) qui contient 1.

Pour les autres, c’est le même principe ; il y a juste plus de règles à vérifier. C’est rébarbatif mais pas particulièrement difficile à comprendre.

Algèbre linéaire

Je vais esquiver cette partie de manière magistrale en me contentant de définir les espaces vectoriels. Référez-vous aux ressources pour plus d’informations !

Soit \( (\mathbb{K}, +, \times) \) un corps et \( E \) un ensemble muni d’une opération notée \( + \) et d’une opération de “multiplication” par les éléments de \( \mathbb{K} \) notée \( . \) telle qu’on peut prendre \( \lambda \in \mathbb{K} \) et \( x \in E \) et multiplier les deux pour obtenir \( \lambda . x \).

On dit que \( E \) est un \( \mathbb{K}\!\)-espace vectoriel s’il vérifie les propriétés suivantes:

1. \( (E, +) \) est un groupe commutatif : en plus des propriétés de groupe, on a \[ \forall x,y \in E, x + y = y + x\]
2. L’opération \( . \) est distributive pour les deux opérations d’addition (celle de \( \mathbb{K} \) et celle de \( E \)), i.e.
   pour tous \( \lambda, \mu \in \mathbb{K}, x, y \in E, \) on a : \[ (\lambda + \mu).x = \lambda.x + \mu.y \] \[ \lambda (x + y) = \lambda.x + \lambda.y \]
3. Le neutre de la multiplication de \( \mathbb{K} \) est neutre pour \( . \): \[ \forall x \in E, 1_\mathbb{K}.x = x \]
4. Les deux multiplications . et \( \times \) sont compatibles : \[ \forall \lambda, \mu \in \mathbb{K}, \forall x \in E, \lambda.(\mu.x) = (\lambda \times \mu).x \]

Pas la peine de retenir tout ce charabia : l’essentiel à comprendre est qu’un espace vectoriel est un espace où on peut faire des additions sur des vecteurs (les éléments de \( E \)) et les multiplier par des scalaires (les éléments de \( \mathbb{K} \)).

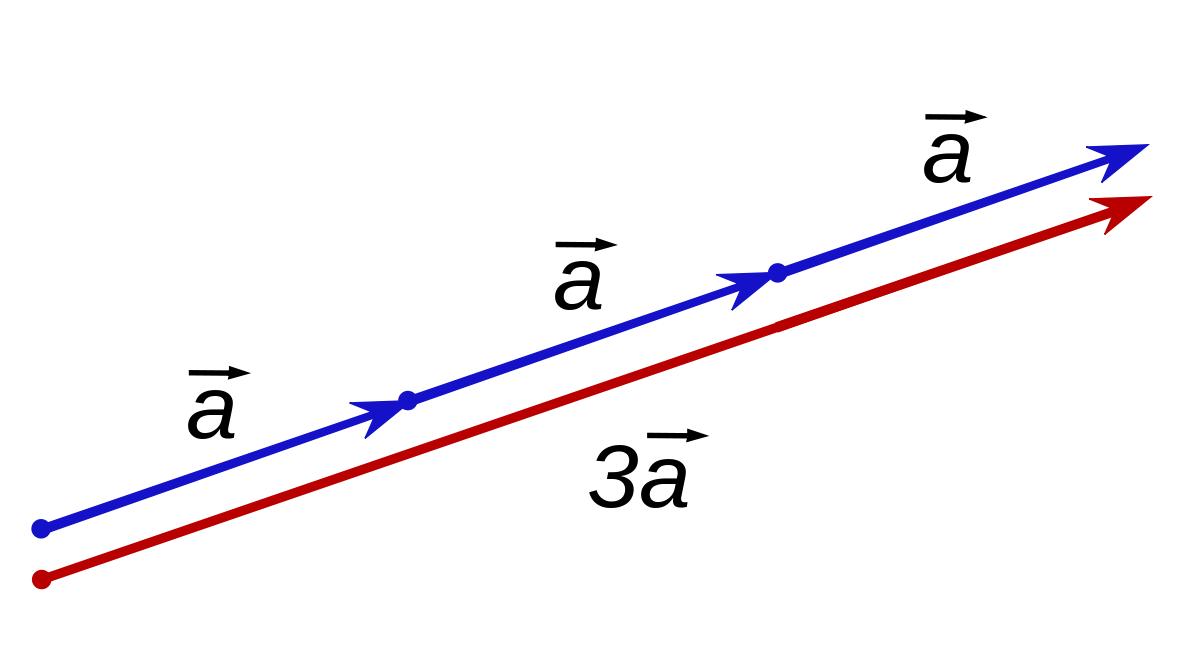
Voyez les vecteurs comme des flèches. Les scalaires sont appelés ainsi parce qu’ils sont utilisés pour échelonner (scale en anglais) les vecteurs. Ainsi, le vecteur \( 2.x \) peut être vu comme deux fois le vecteur \( x \).

Je vais m’arrêter là, mais je ne puis m’empêcher de vous dévoiler une petite pépite qui devrait vous faire sourire si vous avez tout lu jusqu’ici : les espaces vectoriels sont aussi des machins. Même combat !

Ressources

Pour les structures algébriques, je vous conseille la série de Mickaël Launay. Mickaël est bon pédagogue et la série se laisse bien regarder.

Pour l’algèbre linéaire, je ne saurais que vous rediriger vers l'excellente série de 3Blue1Brown. Il vous donne vraiment une bonne intuition des concepts clés : bases, matrices, déterminant…

Dans les deux cours, il n’y a pas de prérequis particulier. Si vous avez le bac général, vous devriez pouvoir suivre sans trop de soucis.